왜 Segment tree를 쓰는가?
Segment라는 단어를 사전에서 찾아보면 '부분, ..을 분할하다' 이런 뜻이 나온다.
말 그대로 구역을 나누어 트리를 만들겠다는 것이다. 무엇을 어떻게 구역으로 나누는가?
가장 흔히 나오는 예시로 배열의 부분합을 구하는 경우를 생각해보자. (세그먼트 트리가 부분합을 구하는데만 사용되는 것은 아니다. 다른 응용문제를 풀어보길 원한다면 BOJ 6549번을 풀어보길 바란다. 내가 세그먼트 트리를 공부하게 된 계기이기도 하다.)
배열 A는 100개의 원소를 가지며, 우리는 i번째부터 j번째 원소의 합을 구하려고한다.
그런데 테스트 케이스가 너무나도 많으므로 매번 i부터 j번째 원소를 더하는 것은 너무 낭비인듯 하다. 그래서 각각의 합(S[i]: 0번째 원소부터 i번째 원소까지의 합)을 미리 계산해두기로 한다.
우리가 흔히 떠올릴 수 있는 방법은 아래와 같다.
S[0] = A[0];
for (int i=1; i<100; i++) {
S[i] = S[i-1] + A[i];
}그리고나서 i부터 j번째까지의 합은 S[j] - S[i-1]를 계산하면 된다. 이 때의 시간 복잡도는 O(N)이다.
그러나 N이 큰 경우에는 시간이 매우 오래 걸리며, 중간에 A의 원소 중 하나라도 변경한다면 S도 전부 다 수정해주어야 하는 번거로움 + 낭비가 발생한다. 다행스럽게도 부분합을 O(logn)만에 구하는 방법이 존재한다.
Segment tree
세그먼트 트리는 말그대로 구역을 나누어 트리를 만드는 것이라고 앞서 말했다. 위의 문제를 해결하고자 우리는 배열 A의 부분 부분의 합들을 트리에 저장하고자 한다. 먼저 어떻게 생겼는지를 살펴보자.
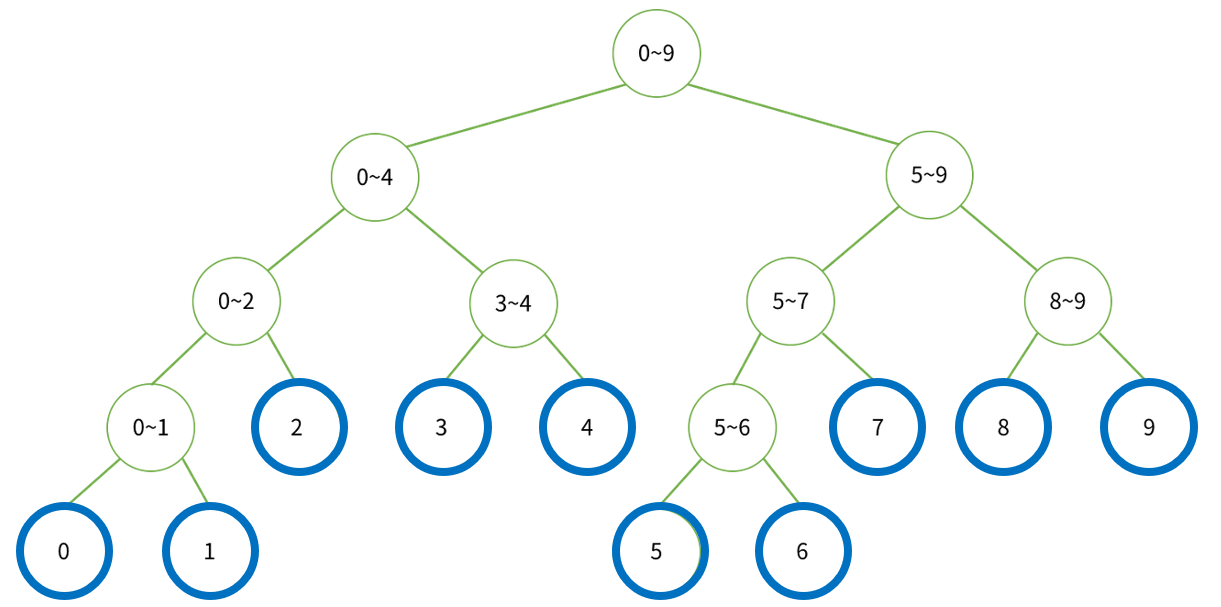
원 안의 숫자들은 A 배열의 인덱스이다. 이 트리 안에는 A 배열에서 해당하는 값들이 들어있다. 2라고 적혀진 원에는 A[2]의 값이 들어있다.
파란색으로 동그라미 쳐있는 것들은 리프 노드라고 한다. 리프 노드는 즉 구역을 나누어 합쳐놓은 것이 아닌 순수 A배열의 원소를 말한다. (그 외의 다른 노드들은 모두 다른 노드라 칭하겠다.) 가령 0~4라고 표시된 다른 노드는 배열 A의 0번째 원소부터 4번째 원소까지의 합이라는 뜻이 된다.
각 노드를 노드 번호로만 표시하면 아래와 같은 그림이 된다.

1) 세그먼트 트리 만들기
위의 그림과 같이 트리를 나타내기 편하다면 좋겠지만, 코드상으로 트리를 나타내는 것은 쉽지 않다. 대신 우리는 비교적 간편한(?) 배열이 있다. (벡터를 배열과 같은 용도로 사용하고 있으므로 앞으로의 글에서 벡터와 배열을 같은 것으로 칭하겠다.)
그림 2를 보여준 이유도 그와 같다. 배열 tree의 인덱스가 저런 모양을 가진 트리로 자리잡는 다는 것을 이해하기 위해서이다. 그럼 우리가 아래 코드에서 만들 tree라는 배열은 그림2 모양으로 생겼으며 그림 1과 같은 내용을 담고 있다고 볼 수 있다.
void init(vector<ll> &a, vector<ll> &tree, int node, int start, int end)
{
if (start == end)
tree[node] = a[start];
else
{
init(a, tree, node * 2, start, (start + end) / 2);
init(a, tree, node * 2 + 1, (start + end) / 2 + 1, end);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
}
// init(a, tree, 1, 0, n-1);로 시작하기코드는 위와 같다. (C++로 작성하였다.) 배열 a를 가지고 tree 노드를 만드는 과정을 보여준다.

이런 배열을 계속 반씩 쪼개서 하나가 될때까지 분할정복(divide and conquer) 하는 과정을 반복한다.
주목할 것은 else 부분에서 init의 node 자리에 각각 node*2, node*+1이 된다는 점인데 그림 2를 보면 쉽게 이해할 수 있다. 부모 노드번호가 i라면 왼쪽 자식의 노드번호는 2*i, 오른쪽 자식의 노드번호는 2*i+1이 된다는 것을 알 수 있다.
나머지는 코드를 찬찬히 살펴보면 이해할 수 있을 것이다.
2) 합 찾기
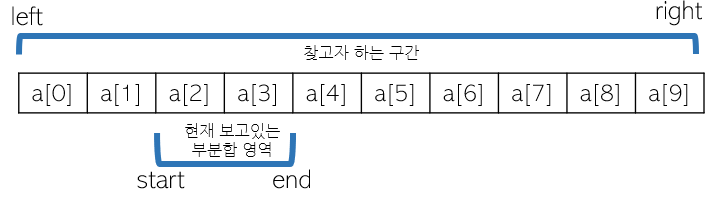
이제 node라는 트리에 적절한 원소들을 담았으니 합을 찾아보자. 우리는 안타깝게도 모든 부분합을 트리에 담고 있지 않다. 그림 1을 보면 알 수 있듯이 총 9개의 부분합 정보를 가지고 있다. 따라서 0~5까지의 부분합은 트리만 가지고 한번에 답을 찾을 수 없다. 찾고자 하는 구간을 left~right라고 해보자.
만약 우리가 보고 있는 tree배열이 0~4의 부분합이라면 우리는 0을 start, 4를 end라고 표기할 것이다.
우리는 배열 A의 left 원소부터 right 원소까지의 부분합을 찾는 것이 목표이다.
생길 수 있는 경우의 수는 다음과 같다.
- [left, right]와 [start, end]가 겹치지 않는 경우
- [left, right]가 [start, end]를 완전히 포함하는 경우
- [start, end]가 [left, right]를 완전히 포함하는 경우
- [left, right]와 [start, end]가 겹쳐져 있는 경우(1, 2, 3 제외한 나머지의 경우)
먼저 1번부터 보자. 가령 [3,4]를 찾는 것이 목적인데, 우리가 보고 있는 노드는 [5,7]의 부분합인 경우가 그렇다. 일반화해서 표현하자면 right < start || end < left인 경우가 1번에 해당한다. 이렇게 되면 완전히 겹치는 부분이 없기 때문에 0을 리턴하고 탐색을 종료하면 된다.

1번의 경우를 그림으로 표현하면 그림 3처럼 된다. 저렇게 되거나 두 파란색 영역이 서로 바뀌어 있을 때가 그렇다.
2번을 보자. 가령 우리는 [0,7]의 합을 알고 싶은데 우리가 보고있는 노드의 부분합은 [3,4]까지이다. 그러나 실제로는 [left, right]가 [start, end]를 넉넉하게(?) 포함하기 전에 둘이 같아지는 순간에서 탐색을 종료해줘야 한다. 그리고나서 그 때의 부분합을 리턴하는 것이다. 이런 경우도 일반화하면 left <= start &&end <= right 로 표현할 수 있다. 이런 경우에는 tree[node]를 리턴하고 탐색을 종료한다.
3번의 경우와 4번의 경우는 아직 start와 end를 더 쪼개서 [left, right] 영역까지 깊이 내려갈 수 있다. 굳이 표현하자면 아래의 그림과 같은 경우가 될 수 있는데, 이 경우에는 start와 end를 더 쪼개서(divide해서) tree 깊숙한 곳까지 내려가야 한다. 따라서 해당 노드의 왼쪽 자식 노드와 오른쪽 자식노드를 더 탐색해봐야 한다.

위의 경우의 수들을 코드로 나타내면 아래와 같다. (C++)
ll sum(vector<ll> &tree, int node, int start, int end, int left, int right)
{
if (right < start || end < left)
return 0;
if (left <= start && end <= right)
return tree[node];
return sum(tree, node * 2, start, (start + end) / 2, left, right) + sum(tree, node * 2 + 1, (start + end) / 2 + 1, end, left, right);
}
3) 배열 A안의 숫자 변경하기
우리가 처음에 for문을 사용한 부분합 대신 세그먼트 트리를 사용한 이유 중 하나가 중간에 배열 A의 값이 바뀔 것을 우려되어서였다. 만약 1부터 10까지의 부분합 S를 구해놨는데 A의 2번째 원소가 변했다면 S의 2~10번째 부분합을 모두 변경해줘야 한다. 총 9번의 값 수정을 해야한다. 너무 비효율적이다.
세그먼트 트리를 사용하면 위의 경우에도 4번의 수정만으로 원하는 목적을 달성할 수 있다.

그림 6을 보면 쉽게 이해할 수 있다. 2번째 원소를 수정하려면 굵은 테두리로 되어있는 네 가지의 숫자만 교체해주면 된다.
교체하는 방법은 무엇일까? 가령 배열 A의 두번째 원소가 8(a[2])이었다고 치자. 우리는 이 값을 5(val)로 바꾸고 싶다. 그렇다면 -3(diff)만큼 더해준 셈이 된다. 자주색 동그라미의 값은 8-3인 5로 교체해주고 파랑색 동그라미에도 모두 -3씩 더해주면 된다.
즉, 해당 index가 포함되는 구간에 diff(=val - a[index])만큼을 전부 더해주면 된다. 아주 간단하다!
따라서 현재 보고있는 [start, end] 안에 index가 포함되면 diff를 더해주고 아니면 거기서 리턴해주면 되는 것이다.
코드는 다음과 같다. (C++)
void update(vector<ll> &tree, int node, int start, int end, int index, ll diff)
{
if (index < start || end < index)
return;
tree[node] += diff;
if (start != end)
{
update(tree, node * 2, start, (start + end) / 2, index, diff);
update(tree, node * 2 + 1, (start + end) / 2 + 1, end, index, diff);
}
}
References
'algorithms' 카테고리의 다른 글
| 문자열로 나타낼 수 있는 순열의 개수(경우의 수) (0) | 2020.02.17 |
|---|---|
| n의 거듭제곱 구하기 (큰 수의 큰 제곱수 구하기) (0) | 2020.01.06 |
| Prim algorithm (프림 알고리즘) (0) | 2019.05.15 |
| Greedy algorithm(탐욕 알고리즘)/ Minimum spanning tree(최소 신장 트리) (0) | 2019.05.14 |

